Monotónní funkce

Monotonie funkce je souhrnný název pro vlastnost funkce být rostoucí nebo klesající, nerostoucí nebo neklesající. Znalost monotonie usnadňuje některé výpočty s funkcemi, například řešení nelineárních nerovnic.

Příklad ryze monotónní (rostoucí) funkce

Definice (monotonie na množině)

Funkce $f$ definovaná na množině $M$ je na této množině rostoucí (též ostře rostoucí nebo ryze rostoucí) právě tehdy, když pro každé dva body $x,y\in M$ platí

$x<y\Rightarrow f(x)<f(y).$

Funkce $f$ definovaná na množině $M$ je na této množině klesající (též ostře klesající nebo ryze klesající) právě tehdy, když pro každé dva body $x,y\in M$ platí

$x<y\Rightarrow f(x)>f(y).$

Funkce $f$ definovaná na množině $M$ je na této množině neklesající právě tehdy, když pro každé dva body $x,y\in M$ platí

$x<y\Rightarrow f(x)\leq f(y).$

Funkce $f$ definovaná na množině $M$ je na této množině nerostoucí právě tehdy, když pro každé dva body $x,y\in M$ platí

$x<y\Rightarrow f(x)\geq f(y).$

Funkce je monotónní na určitém intervalu, množině nebo v celém svém definičním oboru, pokud je na celém daném intervalu, množině, resp. definičním oboru neklesající nebo nerostoucí.

Funkce je ryze monotónní na určitém intervalu, množině nebo v celém svém definičním oboru, pokud je na celém daném intervalu, množině, resp. definičním oboru rostoucí nebo klesající.

Interval, na kterém je funkce ryze monotónní, se nazývá interval monotonie.

Výše uvedené definice popisují globální monotonii. Vlastnost funkce být monotónní bývá nazývána monotónnost, popř. monotonicita.

Příklad

Graf funkce, která na intervalu $\langle A,B\rangle$ není monotónní, ale je monotónní na jeho určitých podintervalech; na intervalu $\langle A,x_{2}\rangle$ a $\langle x_{3},x_{5}\rangle$ je rostoucí, na intervalu $\langle x_{2},x_{3}\rangle$ a $\langle x_{5},B\rangle$ je klesající.

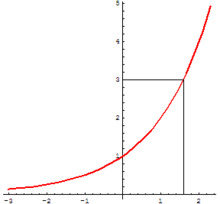
Na obrázku vpravo je funkce rostoucí například v intervalu $\langle x_{3},x_{5}\rangle$, klesající například v intervalu $\langle x_{2},x_{3}\rangle$.

Definice (monotonie v bodě)

Monotonie lokální (v bodě): Funkce je po řadě rostoucí, klesající, neklesající, nerostoucí v bodě $a$, jestliže existuje nějaké okolí $U(a)$ bodu $a$, na kterém je funkce rostoucí, klesající, neklesající, nerostoucí. To je ekvivalentní s tím, že v tomto okolí platí:

• v případě funkce rostoucí v bodě dvojice implikací

$x>a\Rightarrow f(x)>f(a)\quad \land \quad x<a\Rightarrow f(x)<f(a)$,

• v případě funkce klesající v bodě dvojice implikací

$x>a\Rightarrow f(x)<f(a)\quad \land \quad x<a\Rightarrow f(x)>f(a)$,

• v případě funkce nerostoucí v bodě dvojice implikací

$x>a\Rightarrow f(x)\leq f(a)\quad \land \quad x<a\Rightarrow f(x)\geq f(a)$,

• a v případě funkce neklesající v bodě dvojice implikací

$x>a\Rightarrow f(x)\geq f(a)\quad \land \quad x<a\Rightarrow f(x)\leq f(a)$.

Poznámky

• Je zřejmé, že je-li funkce rostoucí, pak je i neklesající. Podobně, je-li funkce klesající, pak je i nerostoucí.
• Ryze monotónní funkce je prostá a má tedy inverzní funkci. Ta má stejný typ monotonie.
• Konstantní funkce je podle výše uvedené definice monotónní, ale není ryze monotónní.

Derivace monotónní funkce

Pokud funkce $f(x)$ má v bodě $a$ derivaci $f^{\prime }(a)$, lze ji použít k vyšetření monotonie funkce, přičemž platí následující implikace (které nelze obrátit):

• Jestliže $f^{\prime }(a)>0$, pak $f(x)$ je v bodě $a$ rostoucí.
• Jestliže $f^{\prime }(a)<0$, pak $f(x)$ je v bodě $a$ klesající.
• Jestliže $f(x)$ je v bodě $a$ neklesající, pak $f^{\prime }(a)\geq 0$.
• Jestliže $f(x)$ je v bodě $a$ nerostoucí, pak $f^{\prime }(a)\leq 0$.

Řešení nerovnic s monotónními funkcemi

Monotonie funkce umožňuje jednotný přístup k práci s nerovnostmi a nerovnicemi.

Přímo z definice plyne, že je-li funkce $f$ rostoucí, potom jsou nerovnosti $x<a$ a $f(x)<f(a)$ ekvivalentní. Toho je možné využít například při řešení nerovnic. Přirozený logaritmus je rostoucí funkce na svém definičním oboru a proto jsou zde ekvivalentní nerovnosti $\ln(x)<\ln(5)$ a $x<5.$ Nerovnice $$\ln(x)<\ln(5)$$ má tedy řešení $$0<x<5.$$(Dolní omezení plyne z definičního oboru přirozeného logaritmu.) Analogické pravidlo platí i pro neostré a opačné nerovnosti.

Je-li funkce klesající, znaménko nerovnosti se otáčí.

Speciálním případem tohoto principu jsou následující pravidla pro práci s nerovnostmi a nerovnicemi.

• K oběma stranám nerovnice můžeme přičíst stejné číslo (funkce $f(x)=x+a$ je rostoucí pro libovolné $a$).
• Obě strany nerovnice můžeme vynásobit stejným kladným číslem (funkce $f(x)=ax$ je rostoucí pro libovolné kladné $a$).
• Obě strany nerovnice můžeme vynásobit stejným záporným číslem a otočit směr nerovnosti (funkce $f(x)=ax$ je klesající pro libovolné záporné $a$).
• Obě strany nerovnice můžeme logaritmovat nebo odlogaritmovat logaritmem o základu větším než jedna.
• Obě strany nerovnice můžeme logaritmovat nebo odlogaritmovat logaritmem o základu menším než jedna a otočit směr nerovnosti.
• Obě strany nerovnice můžeme odmocnit. Pozor, odmocněním nerovnosti $x^{2}<25$ dostáváme nerovnost s absolutní hodnotou $|x|<5$ a oborem pravdivosti $-5<x<5$.

Kvadratická funkce ani převrácená hodnota nejsou ani rostoucí ani klesající funkce. Proto není možno podobnými způsoby řešit kvadratické nerovnice a nerovnice se zlomky. Kvadratická funkce je však rostoucí na množině kladných čísel, proto je možné například tvrdit, že mezi čtverci má největší obsah ten, který má nejdelší stranu. V tomto případě se totiž přirozeně pracuje s kvadratickou funkcí jenom pro kladné hodnoty (délka strany není záporná) a tam je kvadratická funkce udávající vztah mezi délkou strany a obsahem rostoucí.

Další využití monotonie

Kromě řešení nerovnic a práce s nerovnostmi má monotonie následující využití.

Lokální extrémy funkce

• Je-li funkce v nějakém bodě spojitá a mění se zde z rostoucí na klesající, je v tomto bodě ostré lokální maximum. Analogicky, pokud se funkce v bodě mění spojitě z klesající na rostoucí, je v tomto bodě ostré lokální minimum.
• Je-li funkce $g$ libovolná ostře rostoucí funkce, mají funkce $f$ a složená $g\circ f$ lokální extrémy ve stejných bodech. Například tedy lokální maximum funkce $e^{4x-x^{2}}$je ve stejném bodě, jako lokální maximum funkce $4x-x^{2}$, což vede při hledání tohoto maxima na jednodušší postup.

Stabilita stacionárních bodů autonomní diferenciální rovnice

• Autonomní diferenciální rovnice má v bodech, kde je pravá strana nulová, konstantní řešení. Monotonie pravé strany rozhoduje o tom, která z těchto konstantních řešení jsou stabilní a která nestabilní.

Terminologie

Někteří autoři používají termín rostoucí bez přívlastku pro funkce, které jsou ve výše uvedené definici nazývány neklesající a klesající pro funkce podle uvedené definice nerostoucí.

Odkazy

Související články

• Funkce (matematika)
• Derivace

Portály: Matematika