Diracovo delta
funkce, která má v jednom bodě hodnotu nekonečno a v ostatních je identická nule
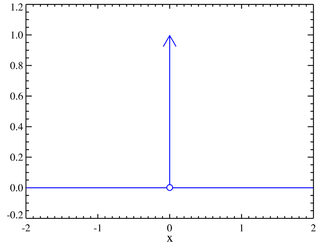
Diracovo delta nebo Diracova -funkce se dá neformálně popsat jako funkce, která má v nule hodnotu nekonečno a všude jinde nulovou. Je značena řeckým písmenem delta. Její integrál přes celý prostor je roven jedné.

- , kde H znamená Heavisideovu funkci
V souvislosti se zpracováním signálu bývá Diracova funkce označována také jako Diracův jednotkový impuls. (Jednotkový právě pro integrál rovný jedné)
Matematicky přesná definice je, že Diracova delta není funkce, ale distribuce. Diskrétním ekvivalentem Diracova delta je Kroneckerovo delta.
Vyjádření editovat
Diracovu -funkci lze vyjádřit různými způsoby. Pro komplexní čísla například ve tvaru integrálu.
Nebo pomocí limit.
Vlastnosti editovat
Označení posunuté („doprava“) delta funkce:
- Delta funkce je sudá funkce.
- Působí jako jednotkový operátor při integraci.
- Konvoluce libovolné funkce s delta funkcí je rovna této funkci.
- Konvoluce s posunutou delta funkcí má za následek posunutí této funkce.
- Fourierova transformace delta funkce je rovna jednotkové funkci.
- Z toho plyne, že zpětná Fourierova transformace jednotkové funkce je ve smyslu distribuce rovna delta funkci.
- Pro Fourierovu transformaci posunuté delta funkce platí:
- Další vztahy[zdroj?]:
Odkazy editovat
Reference editovat
Související články editovat
Externí odkazy editovat
- Obrázky, zvuky či videa k tématu Diracovo delta na Wikimedia Commons
- Diracovo delta v encyklopedii MathWorld (anglicky)




