Meneláova věta

Meneláova věta je tvrzení afinní geometrie o trojúhelnících tradičně připisované starořeckému matematikovi Menelaovi Alexandrijskému. Je duální k Cévově větě.

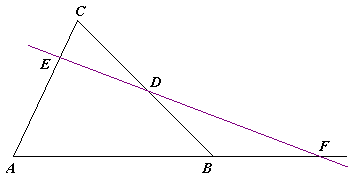
Příklad přímky EDF v případě, kdy protíná trojúhelník

Příklad přímky EDF v případě, kdy neprotíná trojúhelník

Znění Meneláovy věty

Máme-li dány body A,B a C, které tvoří trojúhelník ABC, a jiné body D, E a F, které leží na přímkách BC, AC a AB, pak body D, E a F leží na přímce právě tehdy, když platí

{\frac {AF}{FB}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}=1

V tomto výrazu uvažujeme délky úseček se znaménkem, které je dáno tím, nacházejí-li se body D, E a F uvnitř patřičných úseček, nebo vně. Například podíl AF/FB je kladný právě tehdy, pokud bod F leží na úsečce AB.

Důkaz

Nejdříve ověříme znaménko levé strany a ukážeme, že musí být vždy záporné. To plyne z toho, že přímka buď trojúhelník neprotne vůbec, nebo jej protne právě ve dvou bodech (viz Paschův axiom). Na levé straně je tedy lichý počet záporných zlomků a jejich součin bude vždy záporný.

Spustíme kolmice a, b a c z bodů A, B a C na přímku DEF. Z podobnosti trojúhelníků plyne, že

{\frac {|AF|}{|BF|}}={\frac {a}{b}}

{\frac {|BD|}{|CD|}}={\frac {b}{c}}

{\frac {|CE|}{|AE|}}={\frac {c}{a}}

tedy

\left|{\frac {AF}{FB}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}\right|=\left|{\frac {abc}{abc}}\right|=1

Ještě zbývá dokázat, že pokud by body na přímce neležely, pak rovnost neplatí. Uvažujme bod X na přímce AB, který je různý od bodu F. Označme AF, AX a AB po řadě jako n, n', s. Předpokládejme, že rovnost platí i pro X. Pak platí

{\frac {AF}{FB}}={\frac {AX}{XB}},

neboli

{\frac {n}{s-n}}={\frac {n'}{s-n'}},

odkud uvedením na společného jmenovatele a zjednodušením dostaneme $n=n'$ . Tedy $F=X$ , čímž je důkaz hotov.

Externí odkazy

Obrázky, zvuky či videa k tématu Meneláova věta na Wikimedia Commons
Meneláova věta Archivováno 9. 2. 2007 na Wayback Machine. — na PlanetMath (anglicky)
Meneláova věta — na Mathworldu (anglicky)